• Orthographic Projection
• Stereographic Projection
• Gnomonic Projection
• General Perspective Projection
• Lambert Azimuthal Equal-Area Projection
• Azimuthal Equidistant
• Modified-Stereographic Conformal

Single page version

AZIMUTHAL AND RELATED MAP PROJECTIONS #

A third very important group of map projections, some of which have been known for 2,000 years, consists of five major azimuthal (or zenithal) projections and various less-common forms. While cylindrical and conic projections are related to cylinders and cones wrapped around the globe representing the Earth, the azimuthal projections are formed onto a plane which is usually tangent to the globe at either pole, the Equator, or any intermediate point. These variations are called the polar, equatorial (or meridian or meridional), and oblique (or horizon) aspects, respectively. Some azimuthals are true perspective projections; others are not. Although perspective cylindrical and conic projections are much less used than those which are not perspective, the perspective azimuthals are frequently used and have valuable properties. Complications arise when the ellipsoid is involved, but it is used only in special applications that are discussed below.

As stated earlier, azimuthal projections are characterized by the fact that the direction, or azimuth, from the center of the projection to every other point on the map is shown correctly. In addition, on the spherical forms, all great circles passing through the center of the projection are shown as straight lines. Therefore, the shortest route from this center to any other point is shown as a straight line. This fact made some of these projections especially popular for maps as flight and radio transmission became commonplace.

The five principal azimuthals are as follows:

1. Orthographic. A true perspective, in which the Earth is projected from an infinite distance onto a plane. The map looks like a globe, thus stressing the roundness of the Earth.
2. Stereographic. A true perspective in the spherical form, with the point of perspective on the surface of the sphere at a point exactly opposite the point of tangency for the plane, or opposite the center of the projection, even if the plane is secant. This projection is conformal for sphere or ellipsoid, but the ellipsoidal form is not truly perspective.
3. Gnomonic. A true perspective, with the Earth projected from the center onto the tangent plane. All great circles, not merely those passing through the center, are shown as straight lines on the spherical form.
4. Lambert Azimuthal Equal-Area. Not a true perspective. Areas are correct, and the overall scale variation is less than that found on the major perspective azimuthals.
5. Azimuthal Equidistant. Not a true perspective. Distances from the center of the projection to any other point are shown correctly. Overall scale variation is moderate compared to the perspective azimuthals.

A sixth azimuthal projection of increasing interest in the space age is the general Vertical Perspective (resembling the Orthographic), projecting the Earth from any point in space, such as a satellite, onto a tangent or secant plant. It is used primarily in derivations and pictorial representations.

As a group, the azimuthals have unique esthetic qualities while remaining functional. There is a unity and roundness of the Earth on each (except perhaps the Gnomonic) which is not as apparent on cylindrical and conic projections.

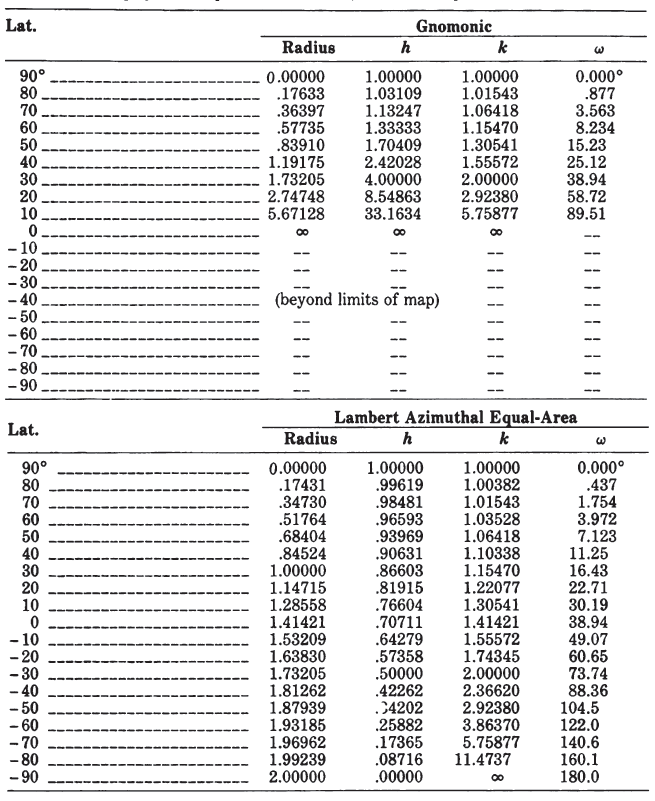
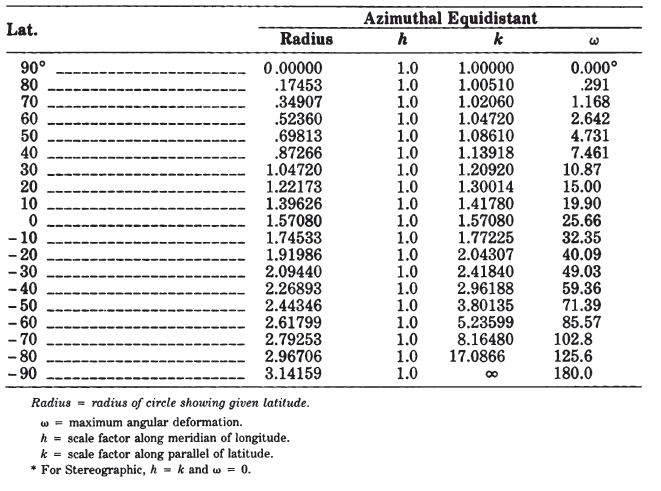
The simplest forms of the azimuthal projections are the polar aspects, in which all meridians are shown as straight lines radiating at their true angles from the center, while parallels of latitude are circles, concentric about the pole. The difference is in the spacing of the parallels. Table 21 lists for the five principal azimuthals the radius of every 10° of latitude on a sphere of radius 1.0 unit, centered on the North Pole. Scale factors and maximum angular deformation are also shown. The distortion is the same for the oblique and equatorial aspects at the same angular distance from the center of the projection, except that h and k are along and perpendicular to, respectively, radii from the center, not necessarily along meridians or parallels.

There are two principal drawbacks to the azimuthals. First, they are more difficult to construct than the cylindricals and the conics, except for the polar aspects. This drawback was more applicable, however, in the days before computers and plotters, but it is still more difficult to prepare a map having complex curves between plotted coordinates than it is to draw the entire graticule with circles and straight lines. Nevertheless, an increased use of azimuthal projections in atlases and for other published maps may be expected.

Secondly, most azimuthal maps do not have standard parallels or standard meridians. Each map has only one standard point: the center (except for the Stereographic, which may have a standard circle). Thus, the azimuthals are suitable for minimizing distortion in a somewhat circular region such as Antarctica, but not for an area with predominant length in one direction.