21. STEREOGRAPHIC PROJECTION #

SUMMARY #

• Azimuthal.
• Conformal.
• The central meridian and a particular parallel (if shown) are straight lines.
• All meridians on the polar aspect and the Equator on the equatorial aspect are straight lines.
• All other meridians and parallels are shown as arcs of circles.
• A perspective projection for the sphere.
• Directions from the center of the projection are true (except on ellipsoidal oblique and equatorial aspects).
• Scale increases away from the center of the projection.
• Point opposite the center of the projection cannot be plotted.
• Used for polar maps and miscellaneous special maps.
• Apparently invented by Hipparchus (2nd century B.C.).

HISTORY #

The Stereographic projection was probably known in its polar form to the Egyptians, while Hipparchus was apparently the first Greek to use it. He is generally considered its inventor. Ptolemy referred to it as “Planisphaerum,” a name used into the 16th century. The name “Stereographic” was assigned to it by François d’Aiguillon in 1613. The polar Stereographic was exclusively used for star maps until perhaps 1507, when the earliest-known use for a map of the world was made by Walther Ludd (Gaultier Lud) of St. Dié, Lorraine.

The oblique aspect was used by Theon of Alexandria in the fourth century for maps of the sky, but it was not proposed for geographical maps until Stabius and Werner discussed it together with their cordiform (heart-shaped) projections in the early 16th century. The earliest-known world maps were included in a 1583 atlas by Jacques de Vaulx (c. 1555-97). The two hemispheres were centered on Paris and its opposite point, respectively.

The equatorial Stereographic originated with the Arabs, and was used by the Arab astronomer Ibn-el-Zarkali (1029-87) of Toledo for an astrolabe. It became a basis for world maps in the early 16th century, with the earliest-known examples by Jean Roze (or Rotz), a Norman, in 1542. After Rumold (the son of Gerardus) Mercator’s use of the equatorial Stereographic for the world maps of the atlas of 1595, it became very popular among cartographers (Keuning, 1955, p. 7-9; Nordenskiöld, 1889, p. 90, 92-93).

FEATURES #

Like the Orthographic, the Stereographic projection is a true perspective in its spherical form. It is the only known true perspective projection of any kind that is also conformal. Its point of projection is on the surface of the sphere at a point just opposite the point of tangency of the plane or the center point of the projection (fig. 31). Thus, if the North Pole is the center of the map, the projection is from the South Pole. All of one hemisphere can be comfortably shown, but it is impossible to show both hemispheres in their entirety from one center. The point on the sphere opposite the center of the map projects at an infinite distance in the plane of the map.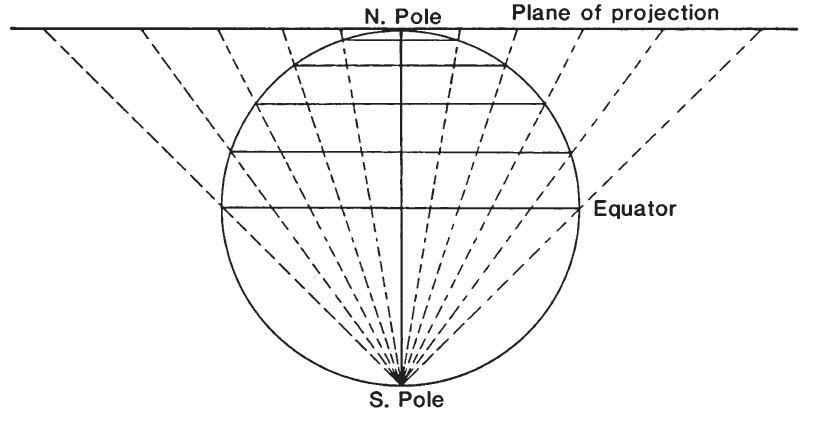

The polar aspect somewhat resembles other polar azimuthals, with straight radiating meridians and concentric circles for parallels (fig. 32A). The parallels are spaced at increasingly wide distances, the farther the latitude is from the pole (the Orthographic has the opposite feature).

In the equatorial and oblique aspects, the distinctive appearance of the Stereographic becomes more evident: All meridians and parallels, except for two, are shown as circles, and the meridians intersect the parallels at right angles (figs. 32B, C). The central meridian is shown straight, as is the parallel of the same numerical value, but opposite in sign to the central parallel. For example, if lat. 40° N. is the central parallel, then lat. 40° S. is shown as a straight line. For the equatorial aspect with lat. 0° as the central parallel, the Equator, which is of course also its own negative counterpart, is shown straight. (For the polar aspect, this has no meaning since the opposite pole cannot be shown.) Circles for parallels are centered along the central meridian; circles for meridians are centered along the straight parallel. The meridian 90° from the central meridian on the equatorial aspect is shown as a circle bounding the hemisphere. This circle is centered on the projection center and is equidistantly marked for parallels of latitude.

As an azimuthal projection, directions from the center are shown correctly in the spherical form. In the ellipsoidal form, only the polar aspect is truly azimuthal, but it is not perspective, in order to retain conformality. The oblique and equatorial aspects of the ellipsoidal Stereographic, in order to be conformal, are neither azimuthal nor perspective. As with other azimuthal projections, there is no distortion at the center, which may be made the “standard point” true to scale in all directions. Because of the conformality of the projection, a Stereographic map may be given, instead of a “standard point,” a “standard circle” (or “standard parallel” in the polar aspect) with an appropriate radius from the center, balancing the scale error throughout the map. (On the ellipsoidal oblique or equatorial aspects, the lines of constant scale are not perfect circles.) This cannot be done with non-conformal azimuthal projections. The Stereographic may also be modified to produce oval and irregular lines of true scale (see p. 203).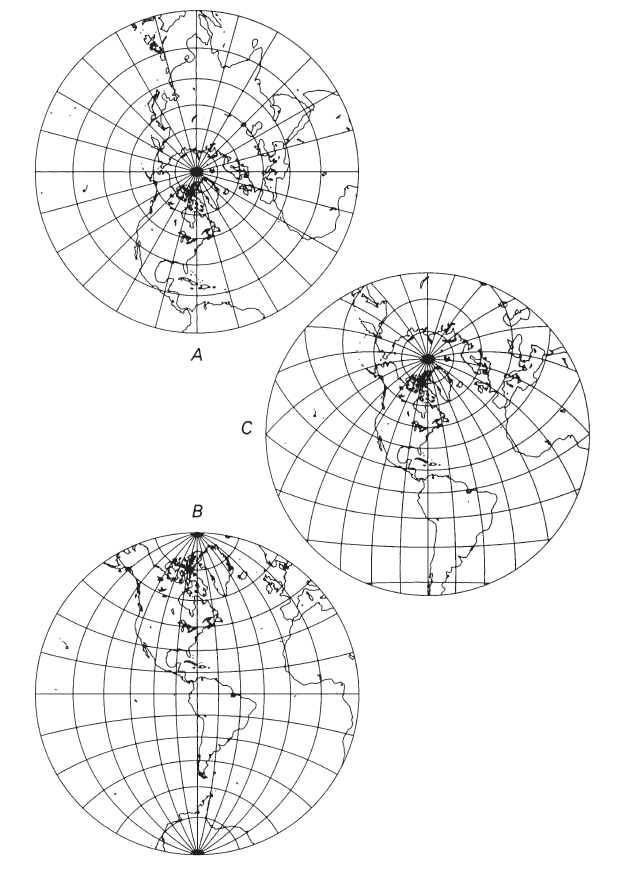

USAGE #

The oblique aspect of the Stereographic projection has been recently used in the spherical form by the USGS for circular maps of portions of the Moon, Mars, and Mercury, generally centered on a basin. The USGS is currently using the spherical oblique aspect to prepare 1:10,000,000-scale maps of Hydrocarbon Provinces for three continents after a least-squares analysis of over 100 points on each continent to determine optimum parameters for a common conformal projection. For Europe, the central scale factor is 0.976 at a central point of lat. 55°N. and long. 20°E. For Africa, these parameters are 0.941, 5° N., and 20° E. For Asia, they are 0.939, 45° N., and 105° E., respectively.

The USGS has most often wed the Stereographic in the polar aspect and ellipsoidal form for maps of Antarctica. For 1:500,000 sketch maps, the standard parallel is 71° S.; for its 1:250,000-scale series between 80° and the South Pole, the standard parallel is 80°14’ S. The Universal Transverse Mercator (UTM) grid employs the UPS (Universal Polar Stereographic) projection from the North Pole to lat. 84° N., and from the South Pole to lat. 80° S. For the UPS, the scale at each pole is reduced to 0.994, resulting in a standard parallel of 81°06'52.3" N. or S. The UPS central meridian (as defined for $\lambda_0$ on p. ix) is the Greenwich meridian, with false eastings and northings of 2,000,000 m at each pole.

In 1962, a United Nations conference changed the polar portion of the International Map of the World (at a scale of 1:1,000,000) from a modified Polyconic to the polar Stereographic. This has consequently affected IMW sheets drawn by the USGS. North of lat. 84° N. or south of lat. 80° S., it is used “with scale matching that of the Modified Polyconic Projection or the Lambert Conformal Conic Projection at Latitudes 84° N. and 80° S.” (United Nations, 1963, p. 10). The reference ellipsoid for all these polar Stereographic projections is the International of 1924.

The Astrogeology Center of the Geological Survey at Flagstaff, Ariz., has been using the polar Stereographic for the mapping of polar areas of every planet and satellite for which there is sufficient information in this region (see table 6).

The USGS is preparing a geologic map of the Arctic regions, using as a base an American Geographical Society map of the Arctic at a scale of 1:5,000,000. Drawn to the Stereographic projection, the map is based on a sphere having a radius which gives it the same volume as the International ellipsoid, and lat. 71° N. is made the standard parallel.

FORMULAS FOR THE SPHERE #

Mathematically, a point at a given angular distance from the chosen center point on the sphere is plotted on the Stereographic projection at a distance from the center proportional to the trigonometric tangent of half that angular distance, and at its true azimuth, or, if the central scale factor is 1,

If $\phi = -\phi_1$, and $\lambda=\lambda_0\pm180^\circ$, the point cannot be plotted. Geometrically, it is the point from which projection takes place. For the north polar Stereographic, with $\phi_1=90°$, these simplify to

For the inverse formulas for the sphere, given $R, k_0, \phi_1, \lambda_0, x,$ and $y$:

If $\phi_1$ is not $\pm90^\circ$:

If $\phi_1$ is $90^\circ$:

The similarity of formulas for Orthographic, Stereographic, and other azimuthals may be noted. The equations for $k’$ ($k$ for the Stereographic, $k’ = 1.0$ for the Orthographic) and the inverse $c$ are the only differences in forward or inverse formulas for the sphere. The formulas are repeated for convenience, unless shown only a few lines earlier.

Table 24 lists rectangular coordinates for the equatorial aspect for a 10° graticule with a sphere of radius $R = 1.0$.

Following are equations for the centers and radii of the circles representing the meridians and parallels of the oblique Stereographic in the spherical form:
Circles for meridians:

To use a “standard circle” for the spherical Stereographic projection, such that the scale error is a minimum (based on least squares) over the apparent area of the map, the circle has an angular distance $c$ from the center, where

FORMULAS FOR THE ELLIPSOID #

As noted above, the ellipsoidal forms of the Stereographic projection are nonperspective, in order to preserve conformality. The oblique and equatorial aspects are also slightly nonazimuthal for the same reason. The formulas result from replacing geodetic latitude $\phi$ in the spherical equations with conformal latitude $\chi$ (see equation (3-1), followed by a small adjustment to the scale at the center of projection (Thomas, 1952, p. 14-15, 128-1891. The general forward formulas for the oblique aspect are as follows; given $a, e, k_0, \phi_1, \lambda_0, \phi,$ and $\lambda$ (see numerical examples):

In the equatorial aspect, with the substitution of $\phi_1 = 0$ (therefore $\chi_1 = 0$), x is still found from (21-24) and k from (21-26), but

For the north polar aspect, substitution of $\phi_1= 90^\circ$ (therefore $\chi_1=90^\circ$) into equations (21-27) and (14-15) leads to an indeterminate $A$. To avoid this problem, the polar equations may take the form

For the south polar aspect, the equations for the north polar aspect may be used, but the signs of $x, y, \phi_c, \phi, \lambda,$ and $\lambda_0$ must be reversed to be used in the equations.

For the inverse formulas for the ellipsoid, the oblique and equatorial aspects (where $\phi_1$ is not $\pm90^\circ$) may be solved as follows, given $a, e, k_0, \phi_1, \lambda_0, x,$ and $y$:

To avoid the iteration of (3-4), this series may be used instead:

The inverse equations for the north polar ellipsoidal Stereographic are as follows; given $a, e, \phi_c, k_0$ (if $\phi_c = 90^\circ$), $\lambda_0, x,$ and $y$:

If $\phi_c$ (the latitude of true scale) is 90°,

To avoid iteration, series (3-5) above may be used in place of (7-9), where

Polar coordinates for the ellipsoidal form of the polar Stereographic are given in table 25, using the International ellipsoid and a central scale factor of 1.0.

To convert coordinates measured on an existing Stereographic map (or other azimuthal map projection), the user may choose any meridian for $\lambda_0$ on the polar aspect, but only the original meridian and parallel may be used for $\lambda_0$, and $\phi_1$, respectively, on other aspects.