22. Gnomonic projection

22. GNOMONIC PROJECTION #

SUMMARY #

  • Azimuthal and perspective.
  • All meridians and the Equator are straight lines.
  • All parallels except the Equator and poles are ellipses, parabolas, or hyperbolas.
  • Neither conformal nor equal-area.
  • All great circles are shown as straight lines.
  • Less than one hemisphere may be shown around a given center.
  • No distortion at the center only.
  • Distortion and scale rapidly increase away from the center.
  • Directions from the center are true.
  • Used only in the spherical form.
  • Known by Greeks 2,000 years ago.

HISTORY #

The Gnomonic is the perspective projection of the globe from the center onto a plane tangent to the surface. It was used by Thales (636?-546?B.C.) of Miletus for star maps. Called “horologium” (sundial or clock) in early times, it was given the name “gnomonic” in the 19th century. It has also been called the Gnomic and the Central projection. The name Gnomonic is derived from the fact that the meridians radiate from the pole (or are spaced, on the equatorial aspect) just as the corresponding hour markings on a sundial for the same central latitude. The gnomon of the sundial is the elevated straightedge pointed toward the pole and casting its shadow on the various hour markings as the sun moves across the sky.

FEATURES AND USAGE #

The outstanding (and only useful) feature of the Gnomonic projection results from the fact that each great-circle arc, the shortest distance between any two points on the surface of a sphere, lies in a plane passing through the center of the globe. Therefore, all great-circle arcs project as straight lines on this projection. The scale is badly distorted along such a plotted great circle, but the route is precise for the sphere.

Because the projection is from the center of the globe (fig. 33), it is impossible to show even a full hemisphere with the Gnomonic. Thus, if either pole is the point of tangency and center (the polar aspect), the Equator cannot be shown. Except at the center, the distortion of shape, area, and scale on the Gnomonic projection is so great that it has seldom been used for atlas maps. Historical exceptions are several sets of star maps from the late 18th century and terrestrial maps of 1803. These maps were plotted with the sphere projected onto the six faces of a tangent cube. The globe has also been projected from the mid-16th to the mid-20th centuries, using the Gnomonic projection as well as others, onto the faces of other polyhedra. Generally, the projection is used for plotting great-circle paths, although the USGS has not used the projection for published maps.

FIGURE 33.— Geometric projection of the parallels of the polar Gnomonic projection.

FIGURE 33.— Geometric projection of the parallels of the polar Gnomonic projection.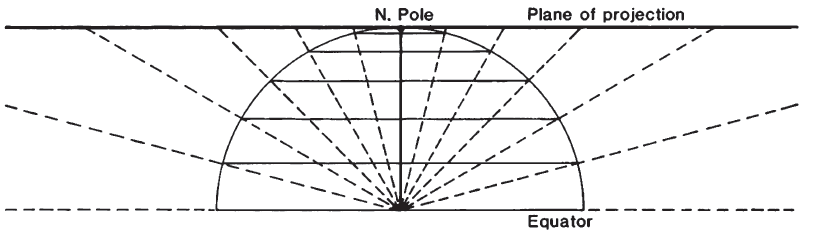

The meridians of the polar Gnomonic projection appear straight, as on other polar azimuthal projections, and parallels of latitude are circles centered about the pole (fig. 34A). The parallels are closest near the pole, and their spacings increase away from the pole much more rapidly than they do on the polar Stereographic. The radii are proportional to the trigonometric tangent of the arc distance from the pole.

On the equatorial aspect, meridians are straight parallel lines perpendicular to the Equator, which is also straight (fig. 34B). The meridians are closest near the central meridian, and the spacing is rapidly increased away from it, the distance from center in proportion to the tangent of the difference in longitude. The parallels other than the Equator are all hyperbolic arcs, symmetrical about the Equator.

Since meridians are great-circle paths, they are also plotted straight on the oblique aspect of the Gnomonic, but they intersect at the pole (fig. 34C). They are not spaced at equal angles. The Equator is a straight line perpendicular to the central meridian. If the central latitude is north of the Equator, its colatitude (90° minus the latitude) is shown as a parabolic arc, more northern latitudes are ellipses, and more southern latitudes are hyperbolas. If the central latitude is south of the Equator, opposite signs apply.

FIGURE 34.— Gnomonic projection, range 60° from center. (A) Polar aspect. (B) Equatorial aspect. (C) Oblique aspect, centered at lat. 40° N. All great-circle paths are straight lines on these maps.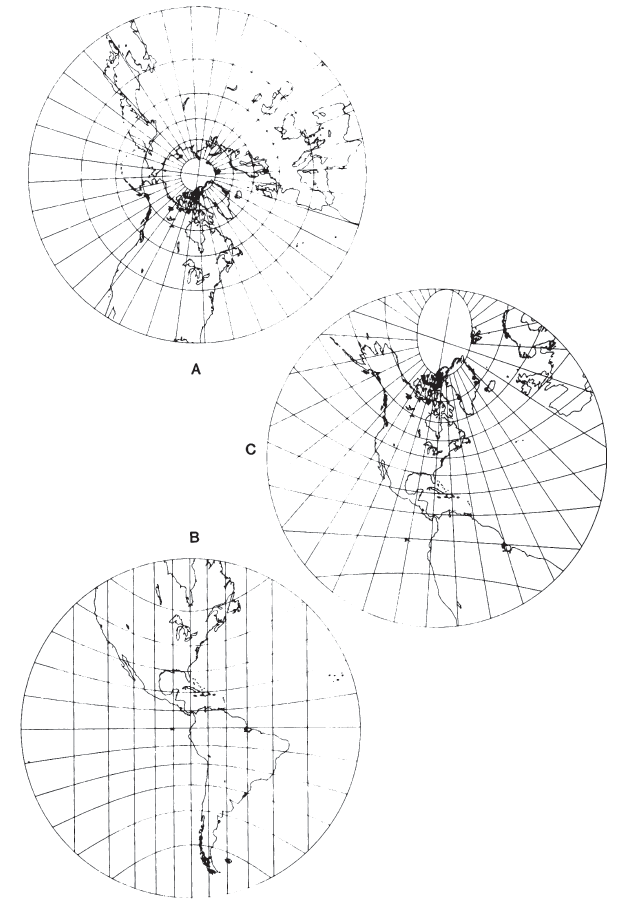

FIGURE 34.— Gnomonic projection, range 60° from center. (A) Polar aspect. (B) Equatorial aspect. (C) Oblique aspect, centered at lat. 40° N. All great-circle paths are straight lines on these maps.

Various graphical constructions have been published, but they are not described here because of the ease of plotting or calculating coordinates by computer, and because they do not add significantly to the understanding of this projection.

FORMULAS FOR THE SPHERE #

A point at a given angular distance from the chosen center point on the sphere is plotted on the Gnomonic projection at a distance from the center proportional to the trigonometric tangent of that angular distance, and at its true azimuth, or

$$ \rho = R \tan{c} \tag{ 22-1 } $$
$$ \theta = \pi-Az = 180^\circ-Az \tag{ 20-2 } $$
$$ h' = 1/\cos^2{c} \tag{ 22-2 } $$
$$ k' = 1/\cos{c} \tag{ 22-3 } $$
where $c$ is the angular distance of the given point from the center of projection. $Az$ is the azimuth east of north, and $\theta$ is the polar coordinate east of south. The term $k’$ is the scale factor in a direction perpendicular to the radius from the center of the map, not along the parallel except on the polar aspect. The scale factor $h’$ is measured in the direction of the radius. Combining with standard equations, the formulas for rectangular coordinates of the oblique Gnomonic projection are as follows, given $R, \phi_1, \lambda_0, \phi,$ and $\lambda$, to find $x$ and $y$ (see numerical examples):
$$ x = R\,k'\,\cos\phi\sin(\lambda-\lambda_0) \tag{ 22-4 } $$
$$ y = R\,k'\,[\cos\phi_1\sin\phi-\sin\phi_1\cos\phi\cos(\lambda-\lambda_0)] \tag{ 22-5 } $$
where $k’$ is found from (22-3) above,
$$ \cos c = \sin\phi_1\sin\phi + \cos\phi_1\cos\phi\cos{(\lambda-\lambda_0)} \tag{ 5-3 } $$
and $(\phi_1, \lambda_0)$ are latitude and longitude of the projection center and origin. The Y axis coincides with the central meridian $\lambda_0,\; y$ increasing northerly. The meridians are straight lines, but the parallels are conic sections for which the eccentricity $=(\cos\phi_1/\sin\phi)$. (If the eccentricity is zero, for $\phi_1 = \pm90^\circ$, they are circles. If the eccentricity is less than 1, they are ellipses; if equal to 1, a parabola; if greater than 1, a hyperbolic arc.)

For the north polar Gnomonic, letting $\phi_1 = 90^\circ$,

$$ x = R\,\cot\phi\sin(\lambda-\lambda_0) \tag{ 22-6 } $$
$$ y = -R\,\cot\phi\cos(\lambda-\lambda_0) \tag{ 22-7 } $$
In polar coordinates,
$$ \rho = R\cot\phi \tag{ 22-8 } $$
$$ \theta = \lambda-\lambda_0 \tag{ 22-9 } $$
For the south polar Gnomonic, with $\phi_1=-90^\circ$,
$$ x = -R\,\cot\phi\sin(\lambda-\lambda_0) \tag{ 22-10 } $$
$$ y = R\,\cot\phi\cos(\lambda-\lambda_0) \tag{ 22-11 } $$
In polar coordinates,
$$ \rho = -R\cot\phi \tag{ 22-12 } $$
$$ \theta = \pi-\lambda+\lambda_0 \tag{ 22-13 } $$
For the equatorial Gnomonic, letting $\phi_1 = 0$,
$$ x = R\tan(\lambda-\lambda_0) \tag{ 22-14 } $$
$$ y = R\tan\phi/\cos(\lambda-\lambda_0) \tag{ 22-15 } $$
In automatically computing a general set of coordinates for a Gnomonic map, equation (5-3) above should be used to reject points equal to or greater than 90° from the center. That is, if $\cos{c}$ is zero or negative, the point is to be rejected. If $\cos c$ is positive, it may or may not be plotted depending on the desired limits of the map. For the inverse formulas for the sphere, to find $\phi$ and $\lambda$, given $R, \phi_1, \lambda_0, x$ and $y$:
$$ \phi = \arcsin{[\cos{c}\sin\phi_1+(y\sin{c}\cos\phi_1/\rho)]} \tag{ 20-14 } $$
If $\rho=0$, equations (20-14) through (20-17) are indeterminate, but $\phi =\phi_1$, and $\lambda=\lambda_0$. If $\phi_1$ is not ±90°,
$$ \lambda = \lambda_0 + \arctan{[x\sin{c}/(\rho\cos\phi_1\cos{c}-y\sin\phi_1\sin{c})]} \tag{ 20-15 } $$
If $\phi_1$ is 90°,
$$ \lambda = \lambda_0+\arctan{[x/(-y)]} \tag{ 20-16 } $$
If $\phi_1$ is -90°,
$$ \lambda = \lambda_0 + \arctan{(x/y)} \tag{ 20-17 } $$
In equations (20-14) and (20-15),
$$ \rho = (x^2+y^2)^{1/2} \tag{ 20-18 } $$
$$ c = \arctan{(\rho/R)} \tag{ 20-19 } $$
Table 26 lists rectangular coordinates for the equatorial aspect for a 10° graticule with a sphere of radius $R=1.0$.
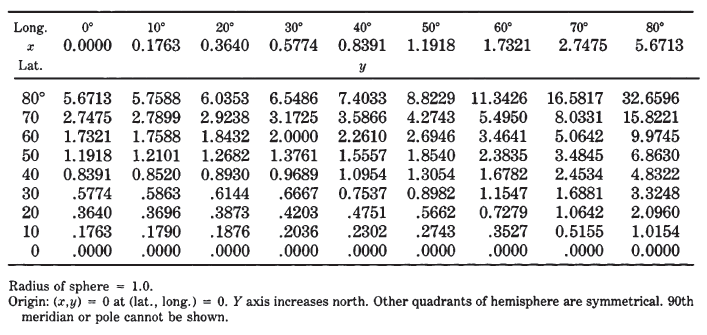
TABLE 26.— Gnomonic projection : Rectangular coordinates for equatorial aspect

TABLE 26.— Gnomonic projection : Rectangular coordinates for equatorial aspect