23. GENERAL PERSPECTIVE PROJECTION #

SUMMARY #

Often used to show the Earth or other planets and satellites as seen from space.
Orthographic, Stereographic, and Gnomonic projections are special forms of the Vertical Perspective.
Vertical Perspective projections are azimuthal; Tilted Perspectives are not.
Central meridian and a particular parallel (if shown) are straight lines.
Other meridians and parallels are usually arcs of circles or ellipses, but some may be parabolas or hyperbolas.
Neither conformal (unless Stereographic) nor equal-area.
If the point of perspective is above the sphere or ellipsoid, less than one hemisphere may be shown, unless the view is from infinity (Orthographic). If below center of globe or beyond the far surface, more than one hemisphere may be shown.
No distortion at the center if a Vertical Perspective is projected onto a tangent plane. Considerable distortion near the projection limit.
Directions from the center are true on the Vertical Perspective for the sphere and for the polar ellipsoidal form.
Known by Greeks and Egyptians 2,000 years ago in limiting forms.

HISTORY AND USAGE #

Whenever the Earth is photographed from space, the camera records the view as a perspective projection. If the camera precisely faces the center of the Earth, the projection is Vertical Perspective. Otherwise, a Tilted Perspective projection is obtained. Perspective views have also served other purposes.

With the complication of plotting coordinates for general perspective projections, there was little known interest in them until the 18th century, except for the well-known special cases of the Orthographic, Stereographic, and Gnomonic projections, which are perspective from infinity, the opposite surface, and the center of the sphere, respectively.

In 1701, the French mathematician Philippe De la Hire (1640-1718) found that if the point of perspective is placed 1.71 times the radius of the globe from the center in a direction opposite that of the plane of projection, the Equator on the polar Vertical Perspective projection has exactly twice the radius of the 45th parallel. The other parallels are not quite proportionally spaced, but this represented a use of geometric projection to achieve low distortion. Several other scientists, such as Antoine Parent in 1702 and various mathematicians of the late 19th century, extended this approach to obtain low-distortion projections which meet other criteria.

Of special interest was British geodesist A.R. Clarke’s use of least squares to obtain in 1862 the Vertical Perspective projection with minimum error for the portion of the Earth bounded by a given spherical circle. He determined parameters for several continental areas, and he also presented the “Twilight” projection, with a bounding circle 108" from the center and centered to show much of the land mass of the Earth in one map. All these low- and minimum-error perspective projections were based on “far-side” points of perspective, and they were projected onto a secant plane to reduce overall error (Close and Clarke, 1911, p. 655-656; Snyder, 1985a).

Space exploration beginning in 1957 led to a renewed interest in the perspective projection, although Richard Edes Harrison had used several perspective views in a World War I1 atlas of 1944. Now the concern was for the pictorial view from space, not for minimal distortion. Albert L. Nowicki of the U.S. Army Map Service presented the AMS Lunar Projection, which is a far-side Vertical Perspective based on a perspective center about 1.54 times the radius from the center, to show somewhat more than one hemisphere of the Moon. This recognized the fact that more than half the Moon is seen from the Earth over a period of time. Nowicki called this a “modified Stereographic” projection (Nowicki, 1962). This name has been applied elsewhere to “far-side” Vertical Perspectives, none of which are conformal; it is applied later in this book to complex-algebra modifications of the Stereographic which are conformal but not perspective.

The Tilted Perspective projection is more complicated to compute, but since it has been the projection used in effect for most space photographs, such as those from the manned Gemini and Apollo space missions, it has been analyzed in recent literature.

Weather maps issued by the U.S. National Weather Service have regularly been based on a Vertical Perspective projection as seen from geosynchronous satellites near the Equatorial plane and 42,000 km from the Earth’s center. The USGS has not used the Perspective projection to date for published maps.

FIGURE 35.— Geometric projection of the parallels of the polar Perspective projections, Vertical and Tilted. Distance of point of perspective from center of Earth may be varied, as may the angle of tilt. For ‘far-side’ projection, ‘point of perspective’ would be shown below Equator and usually below South Pole on this drawing.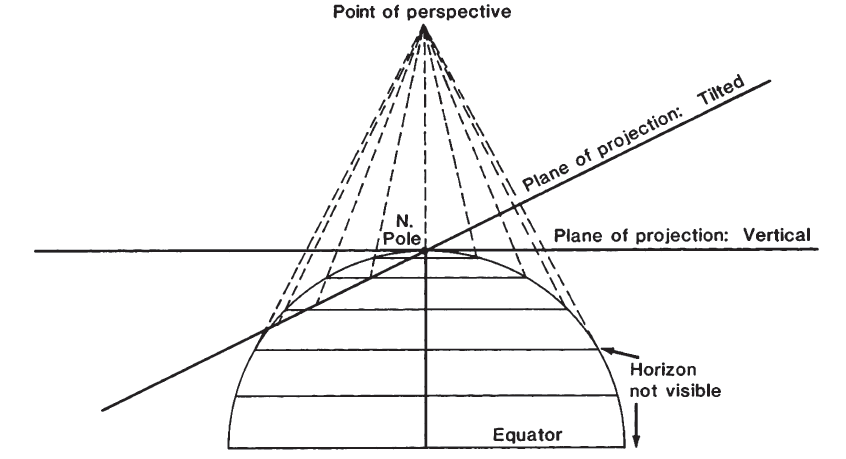 — **FIGURE 35**.— Geometric projection of the parallels of the polar Perspective projections, Vertical and Tilted. Distance of point of perspective from center of Earth may be varied, as may the angle of tilt. For ‘far-side’ projection, ‘point of perspective’ would be shown below Equator and usually below South Pole on this drawing.

FEATURES #

The general Perspective projection (excepting the three common forms) should be considered primarily as a basis for a view of the Earth from space. The various historical studies described above and leading to low-error azimuthal projections have little practical value, since nonperspective azimuthal projections, like the Azimuthal Equidistant, may be used instead.

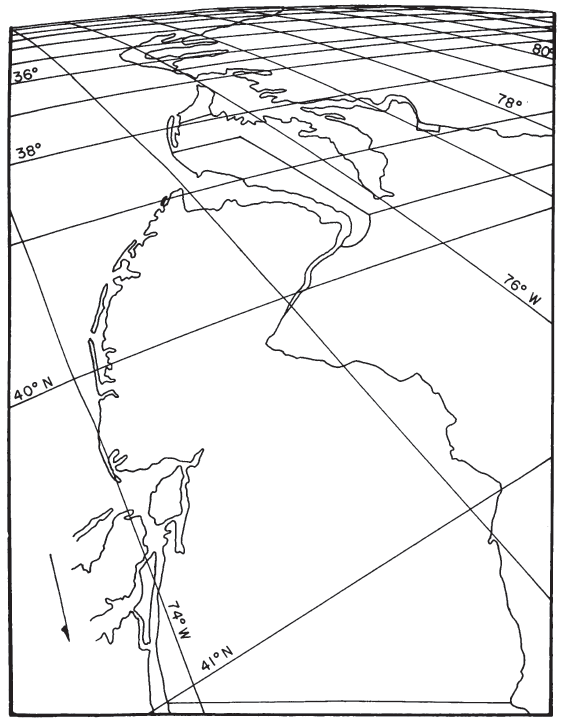
It is therefore of little interest to compute distortion at various locations on the map. There is no distortion at the center of projection with the Vertical Perspective onto a tangent plane (figs. 35 and 36), but there is shape, area, and scale distortion almost everywhere else on perspective maps (except that the Stereographic is conformal). The rapidity with which distortion increases varies with the location of the point of perspective and with the tilt of the plane to the line connecting this point with the center of the Earth (figs. 35 and 37). For the Vertical Perspective, this plane is perpendicular to this line.

FIGURE 36.— Vertical Perspective projection. (A) Polar aspect, from 2,000 km above the Earth’s surface. (B) Equatorial aspect, from geosynchronous satellite, 35,800 km above the Earth’s surface. (C) Oblique aspect, centered at lat. 40° N., from 2,000 km above the Earth’s surface — **FIGURE 36**.— Vertical Perspective projection. (A) Polar aspect, from 2,000 km above the Earth’s surface. (B) Equatorial aspect, from geosynchronous satellite, 35,800 km above the Earth’s surface. (C) Oblique aspect, centered at lat. 40° N., from 2,000 km above the Earth’s surface

While the equations listed below are generally suitable for “far-side” Perspective projections (from below the surface), using negative distances to the points of perspective, the features are described for “near-side” Perspectives. For many perspective maps, one parallel of latitude is shown as a straight line (on the equatorial Orthographic aspect, all are straight). Its location is computed from formulas given below. The central meridian is also straight, as are all meridians on vertical polar aspects. Parallels of latitude on vertical polar aspects are concentric circles. Nearly all other meridians and parallels are elliptical arcs, except that certain angles of tilt may cause some meridians and parallels to be shown as parabolas or hyperbolas.

FIGURE 37.— Tilted Perspective projection. Eastern seaboard viewed from a point about 160 km above Newburgh, N.Y. 1° graticule.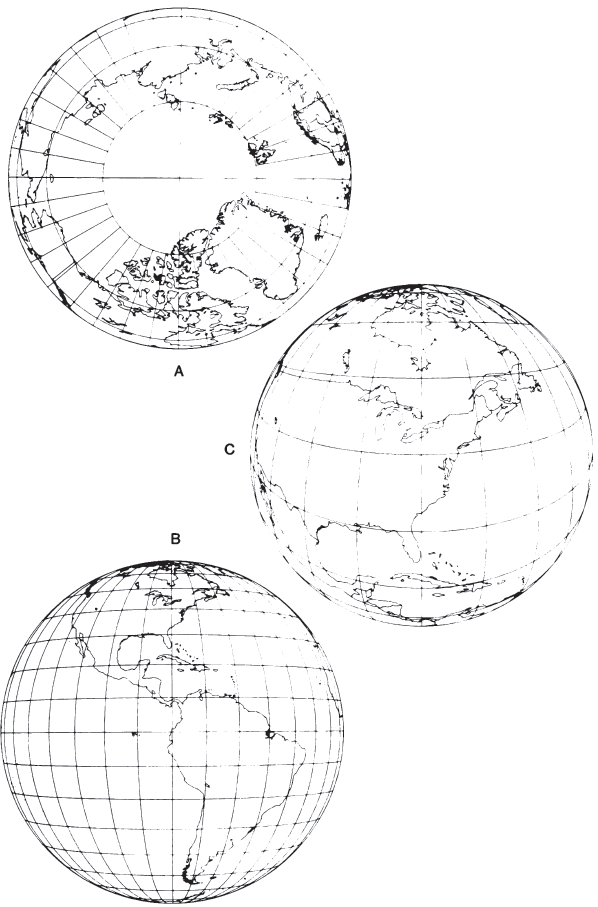 — **FIGURE 37**.— Tilted Perspective projection. Eastern seaboard viewed from a point about 160 km above Newburgh, N.Y. 1° graticule.

The horizon or limit of the map is outlined by one of the conic sections, depending on the angle of tilt and the location of the point of perspective. For the sphere, if there is no tilt, the outline is a circle. It is an ellipse, parabola, or hyperbola if the cosine of the tilt angle is greater than, equal to, or less than, respectively, the radius of the sphere divided by the distance from its center to the point of perspective.

For pictorial and small-scale usage, the spherical equations are adequate. For special large-scale applications, such as Landsat returned-beam-vidicon (RBV) and Space Shuttle Large-Format-Camera images and photographs, the ellipsoidal equations are necessary. The formulas are given below for several possible alternatives.

FORMULAS FOR THE SPHERE #

Vertical Perspective Projection #

A point at a given angular distance $c$ from the center, and at an azimuth $Az$ east of north is plotted in accordance with the following polar coordinates ($\theta$ is measured east of south):

$$ \rho = R(P-I)\sin{c}/(P-\cos{c}) \tag{ 23-1 } $$

$$ \theta = \pi-Az = 180^\circ-Az \tag{ 20-2 } $$

$$ h' = (P-1)(P\cos{c}-1)/(P-\cos{c})^2 \tag{ 23-2 } $$

$$ k' = (P-1)/(P-\cos{c}) \tag{ 23-3 } $$

$P$ is the distance of the point of perspective from the center of the Earth, divided by the radius $R$ of the Earth as a sphere. It is positive in the direction of the center of the projection (for the “view from space”) and negative in the opposite direction (for a far-side perspective such as those by Clarke and Nowicki (above), or the Stereographic, for which $P = -1$). In terms of the height $H$ of the point of perspective above the surface, $P = H/R + 1$, or $H = R(P- 1)$. The term $k’$ is the scale factor in a direction perpendicular to the radius from the center of the map, not along the parallel, except in the polar aspect. The scale factor $h’$ is measured in the direction of the radius.

Combining with standard equations, the formulas for rectangular coordinates of the oblique Vertical Perspective projection are as follows, given $R, P, \chi_1, \lambda_0, \phi$, and $\lambda$, to find $x$ and $y$ (see p. 320 for numerical examples):

$$ x = R\,k'\cos\phi\sin(\lambda-\lambda_0) \tag{ 23-4 } $$

$$ y = R\,k'[cos\phi_1\sin\phi-\sin\phi_1\cos\phi\cos(\lambda-\lambda_0)] \tag{ 23-5 } $$

where $k’$ is found from (23-3) above,

$$ \cos c = \sin\phi_1\sin\phi + \cos\phi_1\cos\phi\cos{(\lambda-\lambda_0)} \tag{ 5-3 } $$

and $(\phi_1, \lambda_0)$ are latitude and longitude of the projection center and origin. The Y axis coincides with the central meridian $\lambda_0$, $y$ increasing northerly. The map limit is a circle of radius $R[(P-1)/(P+1)]^{1/2}$. Meridians and parallels are generally elliptical arcs, but the central meridian and the latitude whose sine equals $P\sin\phi_1$, are straight lines. For automatic plotting, equation (5-3) should be used to reject points for which $\cos{c}$ is less than $1/P$. These are beyond the range of the map, regardless of whether $P$ is positive or negative.

Because of the number of other equations below, the simplified equations for polar and equatorial aspects are not given here. They may be obtained by entering the appropriate values of $\phi_1$, in equations (22-4), (22-5), and (5-3). Table 27 shows rectangular coordinates for a hemisphere as seen from a geosynchronous satellite.

TABLE 27.— Vertical Perspective projection: Rectangular coordinates for equatorial aspect from geosynchronous satellite [y coordinate in parentheses under x coordinate] — **TABLE 27**.— Vertical Perspective projection: Rectangular coordinates for equatorial aspect from geosynchronous satellite [y coordinate in parentheses under x coordinate]

For the inverse formulas for the Vertical Perspective projection of the sphere, given $R, P, \phi_1, \lambda_0, x$ and $y$, to find $\phi$ and $\lambda$:

$$ \phi = \arcsin{[\cos{c}\sin\phi_1+(y\sin{c}\cos\phi_1/\rho)]} \tag{ 20-14 } $$

If $\rho = 0$, equations (20-14) through (20-17) are indeterminate, but $\phi = \phi_1$, and $\lambda = \lambda_0$.

$$ \lambda = \lambda_0 + \arctan{[x\sin{c}/(\rho\cos\phi_1\cos{c}-y\sin\phi_1\sin{c})]} \tag{ 20-15 } $$

In equations (20-14) and (20-15),

$$ \rho = (x^2+y^2)^{1/2} \tag{ 20-18 } $$

$$ \begin{align} c = \arcsin\{&[P-(1-\rho^2(P+1)/(R^2(P-1)))^{1/2}]/ \\ &[R(P-1)/\rho+\rho/(R(P-1))]\} \end{align} \tag{ 23-4 } $$

In (23-4), if $P$ is negative and $\rho$ is greater than $R(P-1)/P$, $c$ must be subtracted from 180° to place it in the proper quadrant.

Tilted Perspective Projection #

The following equations are used in conjunction with the equations above for the Vertical Perspective. While they may be combined, it is easier to follow and more practical to program separately these equations to follow (for forward) or precede (for inverse) those above. For the forward equations, given $R, P, \phi_1, \lambda_0, \omega, \gamma, \phi$, and $\lambda$, $(x,y)$ is first calculated from equations (5-3), (23-3), (22-4), and (22-5) in order, then

$$ x_t = (x\cos\gamma - y\sin\gamma)\cos\omega/A \tag{ 23-5 } $$

$$ y_t = (y\cos\gamma + x\sin\gamma)/A \tag{ 23-6 } $$

where

$$ A = [(y\cos\gamma + x\sin\gamma)\sin\omega/H]+\cos\omega \tag{ 23-7 } $$

$$ H = R(P-1) \tag{ 23-8 } $$

$\gamma$ is the azimuth east of north of the Y axis, the most upward-tilted axis of the plane of projection relative to the tangent plane, and $\omega$ is the upward angle of tilt, or the angle between the $Y_t$ axis and the tangent plane. The $X_t$ axis lies at the intersection of the tangent and tilted planes. The rectangular coordinates $(x_t, y_t)$ lie in the tilted plane, with the origin at $(\phi_1, \lambda_0)$ and the $Y_t$ axis oriented at azimuth $\gamma$ rather than due north (see fig. 38).

FIGURE 38.— Coordinate system for Tilted Perspective projection. The north (N) arrow lies in the vertical plane for the equatorial or oblique aspect. See figure 35 for projection of points onto these planes. — **FIGURE 38**.— Coordinate system for Tilted Perspective projection. The north (N) arrow lies in the vertical plane for the equatorial or oblique aspect. See figure 35 for projection of points onto these planes.

Restated in terms of a camera in space, the camera is placed at a distance $RP$ from the center of the Earth, perpendicularly over point $(\phi_1, \lambda_0)$. The camera is horizontally turned to face $\gamma$ clockwise from north, and then tilted $(90^\circ-\omega)$ downward from horizontal, “horizontal” meaning parallel to a plane tangent to the sphere at $(\phi_1, \lambda_0)$. The photograph is then taken, placing points $(\phi, \lambda)$ in positions $(x_t, y_t)$, based on a scale reduction in $R$. The straight meridian and parallel of the Vertical Perspective are also straight on the Tilted form.

If the tilted plane is perpendicular to the line connecting the point of perspective and the horizon, $\omega = \arcsin (1/P)$. Points for which $\cos{c}$ (equation (5-3)) is less than $(1/P)$ are beyond the map limits, as on the Vertical Perspective, but the map limit is now a conic section of eccentricity equal to $\sin\omega/(1-1/P^2)^{1/2}$. This limit may be plotted by inserting the $(x,y)$ coordinates of the circle representing the Vertical Perspective map limit into equations (23-5) through (23-7) for final plotting coordinates $(x_t, y_t)$, after stating the original equations for the circle in parametric form,

$$ x = R[(P-1)/(P+1)]^{1/2}\sin\theta \tag{ 23-9 } $$

$$ y = R[(P-1)/(P+1)]^{1/2}\cos\theta \tag{ 23-10 } $$

in which $\theta$ is given successive values from 0° to 360°.

For the inverse equations for the Tilted Perspective projection of the sphere, given$R, P, \phi_1, \lambda_0, \omega,\gamma, x_t$ and $y_t$, first $H$ is calculated from (23-8), and $(x,y)$ are calculated from these equations:

$$ M = H x_t/(H - y_t \sin\omega) \tag{ 23-11 } $$

$$ Q = H y_t\cos\omega/(H-y_t\sin\omega) \tag{ 23-12 } $$

$$ x = M\cos\gamma + Q\sin\gamma \tag{ 23-13 } $$

$$ y = Q\cos\gamma -M\sin\gamma \tag{ 23-14 } $$

Then these values of $(x,y)$ are inserted in equations (20-14) through (20-18) and (23-4) for inversing the Vertical Perspective, to obtain $(\phi,\lambda)$.

It is also possible to use projective constants $K_1\,-\,K_{11}$ for the sphere as well as the ellipsoid in equations below, but this is not often done for the sphere. If desired, the formulas below may be used for the sphere if the eccentricity is made zero.

FORMULAS FOR THE ELLIPSOID #

Vertical Perspective Projection #

Because of the increased number of equations, they are given in the order of use. Given $a, e^2, P, \phi_1, \lambda_0, h_0, \phi, \lambda$ and $h$, to find $x$ and $y$ (For numerical examples see p. 323):

$$ N = a/(1-e^2\sin^2{\phi})^{1/2} \tag{ 4-20 } $$

$$ N_1=a/(1-e^2\sin^2\phi_1)^{1/2} \tag{ 8-23 } $$

$$ C = [(N+h)/a]\cos\phi \tag{ 23-15 } $$

$$ S = \{[N(1-e^2)+h]/a\}\sin\phi \tag{ 23-16 } $$

$$ \phi_g = \phi_1-\arcsin[N_1e^2\sin\phi_1\cos\phi_1/(Pa)] \tag{ 23-17 } $$

$$ H = P\,a\cos\phi_g/\cos\phi_1 - N_1-h_0 \tag{ 23-18 } $$

$$ K = H/[P\cos(\phi_1-\phi_g)-S\sin\phi_1-C\cos\phi_1\cos(\lambda-\lambda_0)] \tag{ 23-19 } $$

$$ x = K\,C\sin(\lambda-\lambda_0) \tag{ 23-19a } $$

$$ y = K[P\sin(\phi_1-\phi_g)+S\cos\phi_1-C\sin\phi_1\cos(\lambda-\lambda_0)] \tag{ 23-20 } $$

where
$P =$ the distance of the point of perspective from the center of the Earth, divided by $a$, the semimajor axis.
$H =$ the height of the point of perspective in a direction perpendicular to the surface of the ellipsoid at nadir point $(\phi_1,\lambda_0)$, but measured from the height $h_0$ of the nadir above the ellipsoid, not above sea level.
$\phi_g =$ the geocentric latitude of the point of perspective, measured as the angle between the direct line from the center to this point, and the equatorial plane, not as the geocentric latitude corresponding to $\phi_1$
$h =$ the height of $(\phi,\lambda)$ above the ellipsoid. The use of $h$ makes these formulas more general, but for most plotting of graticules it would be zero.

If $H$ is given rather than $P$, the latter may be computed as follows:

$$ P = (\cos\phi_1/\cos\phi_g)(H+N_1+h_0)/a \tag{ 23-21 } $$

Since $\phi_g$ is calculated from $P$ in equation (23-17), iteration is involved, with $\phi_1$ as the first trial value of $\phi_g$. The comments following the forward formulas for the sphere apply approximately here. The straight parallel is the latitude $\phi$ whose sine equals $P,a\sin\phi_g/[N(1-e^2)+h]$, if $h$ is a constant, such as zero. This is an iterative calculation with successive substitution of $\phi$, starting with $\phi_1$, as a trial. The central meridian $\lambda_0$, is also straight.

For the inverse formulas for the Vertical Perspective projection of the ellipsoid, given $a, e^2, P, \phi_1, \lambda_0, h_0, h, x$ and $y$, to find $\phi, \lambda$: Equations (23-17) and (23-18) are used to compute $\phi_g$ and $H$ (or (23-21) to compute $P$ if $H$ is given), then

$$ B = P\cos(\phi_1-\phi_g) \tag{ 23-22 } $$

$$ D = P\sin(\phi_1-\phi_g) \tag{ 23-23 } $$

$$ L = 1-e^2\cos^2\phi_1 \tag{ 23-24 } $$

$$ G = 1-e^2\sin^2\phi_1 \tag{ 23-25 } $$

$$ J = 2e^2\sin\phi_1\cos\phi_1 \tag{ 23-26 } $$

$$ u = -2BLH-2DGy+BJy+DHJ \tag{ 23-27 } $$

$$ v = LH^2+Gy^2-HJy+(1-e^2)x^2 \tag{ 23-28 } $$

If $h$ is zero, $E = 1$ in the next equation (23-29). If $h$ is not zero, use a first trial $E = 1$. Then,

$$ t = p^2(1-e^2\cos^2\phi_g)-E(1-e^2) \tag{ 23-29 } $$

$$ K' = [-u+(u^2-4tv)^{1/2}]/2t \tag{ 23-30 } $$

$$ X = a[(B-H/K')\cos\phi_1-(y/K'-D)\sin\phi_1] \tag{ 23-31 } $$

$$ Y = ax/K' \tag{ 23-32 } $$

$$ S = (y/K'-D)\cos\phi_1+(B-H/K')\sin\phi_1 \tag{ 23-33 } $$

$$ \lambda = \lambda_0+\arctan(Y/X) \tag{ 23-34 } $$

If $h$ is not zero, $\phi$ may be initially estimated at $\arcsin{S}$ to calculate a trial $\phi$ from equation (23-35) and then $E$ from (23-36). Equations (23-29) through (23-36) are iterated using the latest values of $\phi, E$ and $h$ (based on the height above the ellipsoid at the trial $\phi,\lambda$) until $\phi$ changes by a negligible amount.

$$ \phi = \arcsin\{S/[(1-e^2)/(1-e^2\sin^2\phi)^{1/2}+h/a]\} \tag{ 23-35 } $$

$$ E = [1/(1-e^2\sin^2)^{1/2}+h/a]^2-e^2\sin^2\phi[1/(1-e^2\sin^2)-h^2/(a^2-a^2e^2)] \tag{ 23-36 } $$

If $h$ is zero, no iteration or previous estimate for $\phi$ is necessary, and $\phi$ may be found as follows:

$$ \phi = \arctan\{S/[(1-e^2)(1-e^2-S^2)]^{1/2}\} \tag{ 23-37 } $$

Tilted Perspective Projection Using Projective Equations #

When a photograph or other plane image is obtained from space, projective equations with 11 constants may be used to find the rectangular coordinates of any point of known latitude, longitude, and height above the ellipsoid, in the plane of the image, instead of directly using the orientation of the camera or sensor. The 3-dimensional rectangular coordinates of a point on or off the Earth’s surface can be found from the following equations, taking the semimajor axis $a$ of the Earth as 1.0:

$$ X = C\cos\lambda \tag{ 23-38 } $$

$$ Y = C\sin\lambda \tag{ 23-39 } $$

$$ Z = S \tag{ 23-40 } $$

where $C$ and $S$ are found from equations (23-15) and (23-16) respectively, the X and Y axis lie in the Earth’s equatorial plane, with the X axis intersecting the prime meridian ($\lambda=0$), and the Z axis coincides with the Earth’s polar axis. The values of X, Y, and Z increase from the origin at the center of the Earth toward $\lambda = 0$, $\lambda = 90^\circ$, and the North Pole, respectively, but they are dimensionless in the above equations.

The projective equations are as follows,

$$ x'_t = (K_1X+K_2Y+K_3Z+K_4)/(K_5X+K_6Y+K_7Z+1) \tag{ 23-41 } $$

$$ y'_t = (K_8X+K_9Y+K_{10}Z+K_{11})/(K_5X+K_6Y+K_7Z+1) \tag{ 23-42 } $$

where $(x’_t, y’_t)$ are coordinates in the tilted plane, but relative to any pair of perpendicular axes and any origin, rather than those of $(x_t, y_t)$ as described following (23-8). Constants in the denominators are dimensionless, but those in the numerators are in the same units as $(x’_t, y’_t)$.

The 11 constants $K$, may be determined either from points on the “space photograph” or from the parameters of the “camera.” Although least squares and other corrections are used in determining these constants in analytical photogrammetry for highest precision, the approach given here is confined to the use of measurements which are assumed to the precise. The reader is referred to other texts for the least-squares approach.

To determine $K_1\unicode{x2013}K_{11}$ from six widely spaced identified points on the image, equations (23-41) and (23-42) may be transposed as follows:

$$ XK_1+YK_2+ZK_3-x'_tXK_5-x'_tYK_6-x'_tZK_7 \\ +0K_8+0K_9+0K_{10}+0K_{11} = x'_t \tag{ 23-43 } $$

$$ 0k_1+0K_2+0K_3+0K_4-y'_tXK_5-y'_tYK_6-y'_tZK_7 \\ + XK_8 + YK_9 + ZK_{10}+K_{11} = y'_t \tag{ 23-44 } $$

Using a separate pair of these two equations for each of the six points, and omitting one of the twelve equations, the equations are suitable for solution as eleven simultaneous equations with eleven unknowns ($K_1\unicode{x2013}K_{11}$), using standard programs. A less satisfactory but usable procedure involving only seven simultaneous equations is detailed in Snyder (1981c, p. 158).

To determine $K_1\unicode{x2013}K_{11}$ from parameters of the projection, first $H$ is found from (23-18), then

$$ U = P[\sin(\phi_1-\phi_g)\cos\gamma\sin\omega+\cos(\phi_1-\phi_g)\cos\omega \tag{ 23-45 } $$

$$ F = (\sin\phi_1\sin\lambda_0\cos\gamma - \cos\lambda_0\sin\gamma)/U \tag{ 23-46 } $$

$$ V = (\sin\phi_1\sin\lambda_0\sin\gamma + \cos\lambda_0\cos\gamma)\cos\omega/U \tag{ 23-47 } $$

$$ M = (\sin\phi_1\cos\lambda_0\sin\gamma - \sin\lambda_0\cos\gamma)\cos\omega/U \tag{ 23-48 } $$

$$ N = (\sin\phi_1\cos\lambda_0\cos\gamma + \sin\lambda_0\sin\gamma)/U \tag{ 23-49 } $$

$$ W = (-\sin\gamma\cos\omega\cos\theta - \cos\gamma\sin\theta)/U \tag{ 23-50 } $$

$$ T = (-\sin\gamma\cos\omega\sin\theta + \cos\gamma\cos\theta)/U \tag{ 23-51 } $$

$$ K_5 = -N\sin\omega-\cos\phi_1\cos\lambda_0\cos\omega/U \tag{ 23-52 } $$

$$ K_6 = -F\sin\omega-\cos\phi_1\sin\lambda_0\cos\omega/U \tag{ 23-53 } $$

$$ K_7 = (\cos\phi_1\cos\gamma\sin\omega - \sin\phi_1\cos\omega)/U \tag{ 23-54 } $$

$$ K_1 = H(M\cos\theta + N\sin\theta)+K_5x_0 \tag{ 23-55 } $$

$$ K_2 = H(V\cos\theta + F\sin\theta)+K_6x_0 \tag{ 23-56 } $$

$$ K_3 = HW\cos\phi_1+K_7x_0 \tag{ 23-57 } $$

$$ K_4 = HWP\sin(\phi_1-\phi_g)+x_0 \tag{ 23-58 } $$

$$ K_8 = H(M\sin\theta-N\cos\theta)+K_5y_0 \tag{ 23-59 } $$

$$ K_9 = H(V\sin\theta-F\cos\theta)+K_6y_0 \tag{ 23-60 } $$

$$ K_{10} = HT\cos\phi_1+K_7y_0 \tag{ 23-61 } $$

$$ K_{11} = HTP\sin(\phi_1-\phi_g)+y_0 \tag{ 23-62 } $$

where, to review the meanings of previously defined symbols,
$(\phi_1, \lambda_0) =$ latitude and longitude of the projection center and origin
$\phi_g =$ geocentric latitude of the point of perspective, found from equation (23-17)
$\gamma=$ azimuth east of north of the Y_t axis, or the most upward-tilted axis of the plane of projection
$\omega =$ upward angle of tilt
$P =$ distance from the center of the Earth to the point of perspective, divided by $a$, the semimajor axis.

New symbols are as follows:
$\theta =$ clockwise angle through which the (X_t, Y_t) axes are rotated for the arbitrary axes (X’_t, Y’_t) used for the constants $K_1\unicode{x2013}K_{11}$. This may be made zero to retain the (X_t, Y_t) axes.
$(x_0, y_0) =$ offsets of the (X_t, Y_t) axes to establish a different origin for the (X’_t, Y’_t) axes. They may also be set at zero to retain the (X_t, Y_t) axes.

The two sets of axes are related as follows:

$$ x'_t = x_t\cos\theta-y_t\sin\theta+x_0 \tag{ 23-62a } $$

$$ y'_t = y_t\cos\theta+x_t\sin\theta+y_0 \tag{ 23-62b } $$

For inverse computations using projective constants given $K_1\unicode{x2013}K_{11}, x’_t$ and $y’_t$, to find $\phi$ and $\lambda$, the following are calculated in order:

$$ A_1 = x'_tK_5-K_1 \tag{ 23-63 } $$

$$ A_2 = x'_tK_6-K_2 \tag{ 23-64 } $$

$$ A_3 = x'_tK_7-K_3 \tag{ 23-65 } $$

$$ A_4 = K_4-x'_t \tag{ 23-66 } $$

$$ A_5 = y'_tK_5-K_8 \tag{ 23-67 } $$

$$ A_6 = y'_tK_6-K_9 \tag{ 23-68 } $$

$$ A_7 = y'_tK_7-K_{10} \tag{ 23-69 } $$

$$ A_8 = K_{11}-y'_t \tag{ 23-70 } $$

$$ A_9 = A_1A_8-A_4A_5 \tag{ 23-71 } $$

$$ A_{10} = A_1A_7-A_3A_5 \tag{ 23-72 } $$

$$ A_{11} = A_2A_5-A_1A_6 \tag{ 23-73 } $$

$$ A_{12} = A_2A_7-A_3A_6 \tag{ 23-74 } $$

$$ A_{13} = A_2A_8-A_4A_8 \tag{ 23-75 } $$

$$ A_{14} = {A_{10}}^2+{A_{11}}^2/(1-e^2)+{A_{12}}^2 \tag{ 23-76 } $$

$$ A_{15} = A_9A_{10}+A_{12}A_{13} \tag{ 23-77 } $$

$$ A_{16} = {A_9}^2-E{A_{11}}^2+{A_{13}}^2 \tag{ 23-78 } $$

where $E$ is found from (23-36) if $h$ is not zero, or $E = 1$ if $h$ is zero. Then

$$ S = (A_{15}/A_{14})\pm[(A_{15}/A_{14})^2-A_{16}/A_{14}]^{1/2} \tag{ 23-79 } $$

and $\phi$ is found from (23-35) if $h$ is not zero, or (23-37) if $h$ is zero, taking one sign in (23-79) for the latitude desired, and the opposite sign for the latitude hidden from view at the same coordinates. The same sign applies throughout the map, once it is determined for a point for which the latitude is obviously right or wrong.

$$ \lambda = \arctan[(A_9-A_{10}S)/(A_{12}S-A_{13})] \tag{ 23-80 } $$

In this case the ATAN2 function is not used, but 180° must be added to or subtracted from $h$ if the denominator has the same sign as $A_{11}$.

If $h$ is not zero, $E$ is initially assumed to be 1. After trial values of $\phi$ and $\lambda$ are determined above, an $h$ suitable for that point may be used with the new $\phi$ in calculating $E$; then $A_{16}, S, \phi$ and $\lambda$ are recalculated. Iteration continues until the change in the calculated $\phi$ is negligible.

If $h$ is zero, since $E = 1$ and (23-37) is explicit in $\phi$, no iteration is required.

Finally, to compute “camera” parameters from given constants $K_1\unicode{x2013}K_{11}$ (Bender, ca. 1970, p. 26-27), given $a, e^2$, and an assumed $h_0$, first the following three simultaneous equations are solved for $X_0, Y_0,$ and $Z_0$, the space coordinates of the point of perspective divided by $a$ (see description of axes following (23-40)):

$$ \begin{align} K_1X_0+K_2Y_0+K_3Z_0 &= -K_4 \\ K_8X_0+K_9Y_0+K_{10}Z_0 &= -K_{11} \\ K_5X_0+K_6Y_0+K_7Z_0 &= -1 \end{align} \tag{ 23-8 } $$

Then the coordinates $(x_p, y_p)$ of the principal point of the “space photograph” are found as the point where a perpendicular dropped from the point of perspective strikes the plane of the map:

$$ x_p = (K_1K_5+K_2K_6+K_3K_7)/(K_5^2+K_6^2+K_7^2) \tag{ 23-82 } $$

$$ y_p = (K_5K_8+K_6K_9+K_7K_{10})/(K_5^2+K_6^2+K_7^2) \tag{ 23-83 } $$

The parameters reviewed after equation (23-62) are then found as follows (except that $\phi_g$ is an intermediate latitude described after (23-20)):

$$ \lambda_0 = \arctan(Y_0/X_0) \tag{ 23-84 } $$

$$ P = (X_0^2+Y_0^2+Z_0^2)^{1/2} \tag{ 23-85 } $$

$$ \phi_g = \arcsin(Z_0/P) \tag{ 23-86 } $$

$$ \phi_1 = \phi_g + \arcsin\{e^2\sin\phi_1\cos\phi_1/[P(1-e^2\sin^2\phi_1)^{1/2}]\} \tag{ 23-87 } $$

which is solved for $\phi_1$ with $\phi_g$ the first approximation for $\phi_1$ and iterating with successive substitution.

$$ H = a[P\cos\phi_g/\cos\phi_1-1/(1-e^2sin^2\phi_1)^{1/2}-h_0/a] \tag{ 23-88 } $$

using for $h_0$ the height at $(\phi_1,\lambda_0)$. The forward equations (23-15), (23-16), and (23-38) through (23-40) are now used to calculate $X, Y$, and $Z$ for $(\phi_1, \lambda_0, h_0)$. Substituting these values and $K_1\unicode{x2013}K_{11}$ into (23-41) and (23-42), $x_0$ is found as $x’_t$, and $y_0$ as $y’_t$. Then

$$ \omega = \arcsin\{[(x_0-x_p)^2+(y_p-y_0)^2]^{1/2}/H\} \tag{ 23-89 } $$

$$ \theta = \arctan[(x_0-x_p)/(y_p-y_0)] \tag{ 23-90 } $$

Then, $(x’_t,y’_t)$ are calculated for $(\phi_1+ 0.02^\circ, \lambda_0)$ from (23-41) and (23-42) and the necessary preceding equations, in order to obtain the direction of the Y_t axis, and from this value of $(x’_t,y’_t)$ are calculated

$$ x_t = (x'_t-x_0)\cos\theta + (y'_t-y_0)\sin\theta \tag{ 23-91 } $$

$$ y_t = (y'_t-y_0)\cos\theta - (x'_t-x_0)\sin\theta \tag{ 23-92 } $$

$$ \gamma = -\arctan[x_t/(y_t\cos\omega)] \tag{ 23-93 } $$