A Small, Inconsequential, Mystery

October 27, 2024

In his reference work, Snyder gives the following iterative formula for converting from authalic latitude, $\beta$ to geodetic latitude:

$$ \phi = \phi + \frac{(1-e^2\sin^2{\phi})^2}{2\cos{\phi}}\left[ \frac{q}{1-e^2} - \frac{\sin{\phi}}{1-e^2\sin^2{\phi}} + \frac 1{2e} \ln{\left( \frac{1-e\sin{\phi}}{1+e\sin{\phi}}\right)}\right] \tag{ 3-16 } $$

with $ \phi_0 = \arcsin (q/2) $ as initial value and $q = q_p\sin{\beta} $ (see here).

Snyder says that the above formula is derived from the direct formula using the Newton-Raphson iteration method. It is known that the efficiency and convergence of Newton-Raphson method is highly dependent of the choice of initial value¹. On the other hand, it is also known that difference between geodetic and authalic latitude is quite small, as indicated in the graph below taken from Wikipedia:

So, why not take the value of authalic latitude $\beta$ as initial value?

I did just that and, indeed, the number of iterations remains constant (3) for all latitude values. Meanwhile, using Synder formula, the number of iterations starts increasing as the latitude value goes over $60^\circ$.

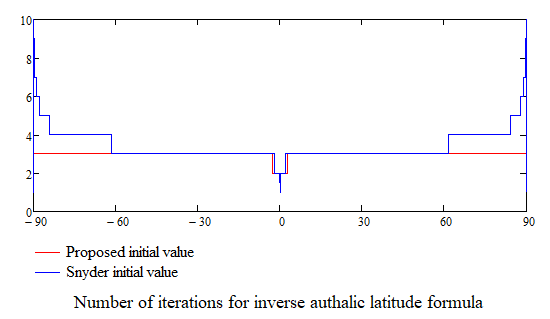
Mussing: I found the same indication for initial value on a number of sites. Critical thinking is not at it’s best.

William H. Press … [and others]. Numerical Recipes in C : the Art of Scientific Computing. Cambridge [Cambridgeshire] ; New York :Cambridge University Press, 1992. page 362-364 ↩︎